Relationships and Graphs

One of the main uses of an ontology is to precisely state the Relationships between different entities or concepts.

In OAK, classes in ontologies can be related to one another via different relationship types, also known as Predicates. These may come from a relationship type ontology such as RO, or they may be a “built-in” construct in RDF or OWL such as rdfs:subClassOf.

These can be thought of as a Graph of concepts and relationships. This is a common idiom for bioinformatics users of ontologies - but, perhaps surprisingly, graphs do not feature heavily in Description Logic formalisms of ontologies like OWL.

Instead there exist a number of different Ontology Graph Projection methods that project from OWL to a graph. The fact there is no one standard method can lead to confusion.

But let’s start with a standard bio-ontology example - the UBERON ontology.

Exploring relationships

Let’s explore Uberon, looking at the relationships for hand (“manus”) and foot (“pes”), which have respective CURIEs UBERON:0002398 and UBERON:0002387.

We will use the relationships method from Basic Ontology Interface.

>>> from oaklib import get_adapter
>>> adapter = get_adapter("sqlite:obo:uberon")
>>> for rel in adapter.relationships(["UBERON:0002398", "UBERON:0002387"]):
...    print(rel)
('UBERON:0002387', 'BFO:0000050', 'UBERON:0002103')
('UBERON:0002387', 'RO:0002202', 'UBERON:0006871')
('UBERON:0002387', 'RO:0002551', 'UBERON:0001445')
('UBERON:0002387', 'rdfs:subClassOf', 'UBERON:0002470')
('UBERON:0002387', 'rdfs:subClassOf', 'UBERON:0008784')
('UBERON:0002398', 'BFO:0000050', 'UBERON:0002102')
('UBERON:0002398', 'RO:0002202', 'UBERON:0006875')
('UBERON:0002398', 'RO:0002551', 'UBERON:0001442')
('UBERON:0002398', 'rdfs:subClassOf', 'UBERON:0002470')
('UBERON:0002398', 'rdfs:subClassOf', 'UBERON:0008785')

Each line is Relationship tuple, (SUBJECT, PREDICATE, OBJECT).

We can make this more human readable:

>>> for s, p, o in adapter.relationships(["UBERON:0002398", "UBERON:0002387"]):
...    print((adapter.label(s), adapter.label(p), adapter.label(o)))
('pes', 'part of', 'hindlimb')
('pes', 'develops from', 'embryonic footplate')
('pes', 'has skeleton', 'skeleton of pes')
('pes', None, 'autopod region')
('pes', None, 'lower limb segment')
('manus', 'part of', 'forelimb')
('manus', 'develops from', 'embryonic handplate')
('manus', 'has skeleton', 'skeleton of manus')
('manus', None, 'autopod region')
('manus', None, 'upper limb segment')

(note subClassOf / IS_A labels are outside the ontology so they have no labels)

Note

if you are used to working with OWL and the underlying RDF/OWL representation the presentation as simple triads above can be confusing, as these are not actually modeled as triples in the ontology, but rather as more complex axioms involving constructs like existential restriction. These axioms are projected onto a graph representation. We will return to this topic later.

Graph Traversal and Relation Graph Reasoning

The above examples show Asserted Relationships between concepts. A common use case for ontologies is exploring indirect or Entailed Relationships, which roughly corresponds to the concept of Ancestor in a graph.

We will use the ancestors method from Basic Ontology Interface.

>>> from oaklib.selector import get_adapter
>>> from oaklib.datamodels.vocabulary import IS_A, PART_OF
>>> adapter = get_adapter("sqlite:obo:uberon")
>>> for anc in sorted(adapter.ancestors("UBERON:0002398", predicates=[IS_A, PART_OF])):
...    print(f"{anc} '{adapter.label(anc)}'")
BFO:0000001 'entity'
BFO:0000002 'continuant'
BFO:0000004 'independent continuant'
BFO:0000040 'material entity'
...
UBERON:0000026 'appendage'
UBERON:0000061 'anatomical structure'
UBERON:0000153 'anterior region of body'
UBERON:0000465 'material anatomical entity'
UBERON:0000468 'multicellular organism'
UBERON:0000475 'organism subdivision'
UBERON:0001062 'anatomical entity'
UBERON:0002101 'limb'
...

Graph Traversal Strategies

There are actually two strategies for getting indirect relationships in OAK:

• HOP, aka Graph Traversal

• ENTAILMENT, aka Reasoning

You can specify which you would like, but if you leave this open the adapter will choose a default. Not all adapters can implement both strategies.

What are the differences? In many cases the results are the same, but formally the differences are:

• HOP yields all nodes that can be traversed via zero or more hops from the specified starting point(s), over the specified relationships

• ENTAILMENT uses deductive reasoning to compute inferred relationships, and yields any relationships whose entailed predicate matches the input list

Currently the following OAK adapters incorporate entailment:

• Ubergraph Adapter

• SQL Database Adapter

In both cases the entailment is done ahead of time using Relation Graph to compute the entailed edges.

Note

We have experimental support for entailment with other adapters, this requires having relation-graph on the command line.

Examples of where entailment yields more

Assuming we have edges:

• A has-part B (in OWL: A SubClassOf has-part some B)

• B part-of C (in OWL: B SubClassOf part-of some C)

And additionally, the ontology contains a Property Chain axiom:

• has-part o part-of -> overlaps

Then using the entailment strategy we get an entailed edge:

• A overlaps C (in OWL: A SubClassOf overlaps some C)

Using graph traversal will tell us that there is at least one path between A and B, and that this path involves hoping over two predicates, but it doesn’t give us precise information about the relationship between A and C.

Furthermore, if we use graph traversal and don’t filter over predicates, then we may end up with lots of essentially meaningless paths, especially if the ontology makes use of extensive relationships from an ontology like RO.

Let’s make this more concrete with a subset of an actual ontology:

[Term]
id: GO:0012505
name: endomembrane system
is_a: GO:0110165 ! cellular anatomical entity
relationship: has_part GO:0005773 ! vacuole

[Term]
id: GO:0005773
name: vacuole
is_a: GO:0043231 ! intracellular membrane-bounded organelle
relationship: part_of GO:0005737 ! cytoplasm

[Term]
id: GO:0043227
name: membrane-bounded organelle
is_a: GO:0043226 ! organelle

[Term]
id: GO:0043229
name: intracellular organelle
is_a: GO:0043226 ! organelle

[Term]
id: GO:0043231
name: intracellular membrane-bounded organelle
is_a: GO:0043227 ! membrane-bounded organelle
is_a: GO:0043229 ! intracellular organelle

[Term]
id: GO:0043226
name: organelle
is_a: GO:0110165 ! cellular anatomical entity

[Term]
id: GO:0005737
name: cytoplasm
is_a: GO:0110165 ! cellular anatomical entity

[Term]
id: GO:0110165
name: cellular anatomical entity

[Typedef]
id: part_of
name: part of
xref: BFO:0000050
is_transitive: true
is_a: overlaps

[Typedef]
id: has_part
name: has part
xref: BFO:0000051
inverse_of: part_of
is_a: overlaps

[Typedef]
id: overlaps
name: overlaps
xref: RO:0002131
holds_over_chain: has_part part_of

We use OBO Format for compactness here, but the same thing that can be done in OWL. Note the holds_over_chain axiom, which is a Property Chain axiom.

The ontology can be visualized:

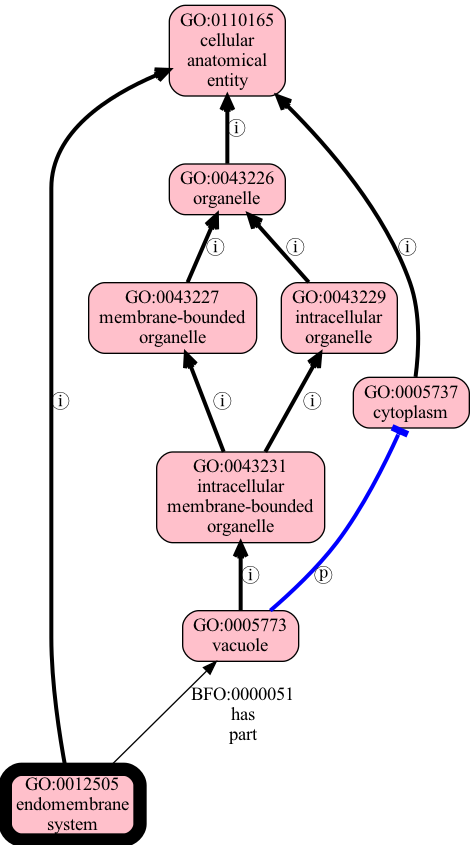
Example sub-ontology focused on the endomembrane system (GO:0012505). This is a simplified subset of GO for demo purposes. Figure generated using runoak viz -i tests/input/entailment-tutorial.obo "endomembrane system"

Let’s load up the ontology:

>>> adapter = get_adapter("simpleobo:tests/input/entailment-tutorial.obo")

Now let’s use the default graph traversal to get the ancestors of GO:0012505 endomembrane system:

>>> len(list(adapter.ancestors("GO:0012505")))
8

This is all the nodes in the graph (including the query node itself, as operations are by default Reflexive).

Now let’s use the entailment strategy to get Entailed ancestors:

>>> from oaklib.interfaces.obograph_interface import GraphTraversalMethod
>>> len(list(adapter.ancestors("GO:0012505", method=GraphTraversalMethod.ENTAILMENT)))
8

Identical results! (Later on we will use an example where the results are different).

One advantage of the entailment strategy is that we can see the inferred relationship between any term pair. To do this, we use the relationships method in Basic Ontology Interface:

>>> for _, p, o in sorted(adapter.relationships(["GO:0012505"],
...                                         include_entailed=True)):
...     print(p, o, adapter.label(o))
BFO:0000051 GO:0005773 vacuole
BFO:0000051 GO:0043226 organelle
BFO:0000051 GO:0043227 membrane-bounded organelle
BFO:0000051 GO:0043229 intracellular organelle
BFO:0000051 GO:0043231 intracellular membrane-bounded organelle
BFO:0000051 GO:0110165 cellular anatomical entity
RO:0002131 GO:0005737 cytoplasm
RO:0002131 GO:0005773 vacuole
RO:0002131 GO:0043226 organelle
RO:0002131 GO:0043227 membrane-bounded organelle
RO:0002131 GO:0043229 intracellular organelle
RO:0002131 GO:0043231 intracellular membrane-bounded organelle
RO:0002131 GO:0110165 cellular anatomical entity
rdfs:subClassOf GO:0012505 endomembrane system
rdfs:subClassOf GO:0110165 cellular anatomical entity

No equivalent operation exists for graph traversal.

However, it is possible to use the paths method to see all paths, e.g. between endomembrane system and cytoplasm:

>>> for _s, _e, node in sorted(adapter.paths(["GO:0012505"],
...                                          directed=True,
...                                          target_curies=["GO:0005737"])):
...     print(node)
GO:0005737
GO:0005773
GO:0012505

This is the list of intermediate nodes.

We can also see a difference if we restrict the graph traversal to specified predicates, e.g. has-part (BFO:0000051):

With the default method:

>>> for a in sorted(adapter.ancestors("GO:0012505",
...                                   predicates=["BFO:0000051"],
...                                   method=GraphTraversalMethod.HOP)):
...     print(a, adapter.label(a))
GO:0005773 vacuole
GO:0012505 endomembrane system

Here the ancestors method is walking the graph, and performing a direct filter on edges.

With entailment

>>> for a in sorted(adapter.ancestors("GO:0012505",
...                                   predicates=["BFO:0000051"],
...                                   method=GraphTraversalMethod.ENTAILMENT)):
...     print(a, adapter.label(a))
GO:0005773 vacuole
GO:0043226 organelle
GO:0043227 membrane-bounded organelle
GO:0043229 intracellular organelle
GO:0043231 intracellular membrane-bounded organelle
GO:0110165 cellular anatomical entity

Here the entailment strategy yields all ancestors A such that the axiom “endomembrane system SubClassOf has-part some A” is true.

This difference is further marked when we query using the overlaps (RO:0002131) relation. Note this is not Asserted in the sample ontology.

>>> list(adapter.ancestors("GO:0012505",
...                        predicates=["RO:0002131"],
...                        reflexive=False,
...                        method=GraphTraversalMethod.HOP))
[]

But if we ask the same question using the entailment strategy, we get everything that overlaps with the endomembrane system:

>>> for a in sorted(adapter.ancestors("GO:0012505",
...                                   predicates=["RO:0002131"],
...                                   reflexive=False,
...                                   method=GraphTraversalMethod.ENTAILMENT)):
...     print(a, adapter.label(a))
GO:0005737 cytoplasm
GO:0005773 vacuole
GO:0043226 organelle
GO:0043227 membrane-bounded organelle
GO:0043229 intracellular organelle
GO:0043231 intracellular membrane-bounded organelle
GO:0110165 cellular anatomical entity

Examples of where graph traversal yields more ancestors than entailment

Let’s extend our ontology by adding an additional edge:

• cytoplasm has-characteristic liquid (PATO:0001735)

Our ontology now looks like:

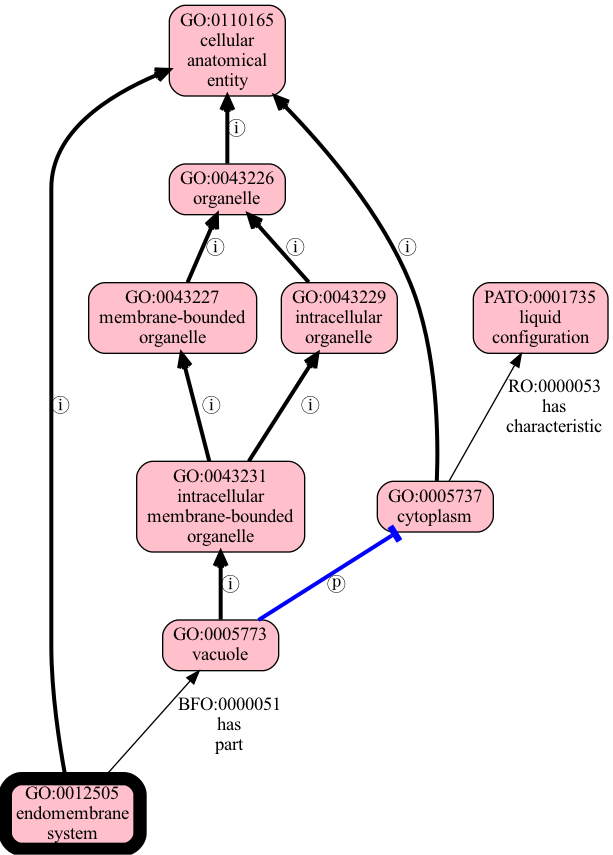
This extends the previous figure by the addition of a new edge with a new predicate (has-characteristic). Figure generated using runoak viz -i tests/input/entailment-tutorial-2.obo

Let’s load up the 2nd ontology:

>>> adapter = get_adapter("simpleobo:tests/input/entailment-tutorial-2.obo")

Let’s compare the results of the two strategies, without filtering for predicates:

>>> hop_ancs = list(adapter.ancestors("GO:0012505",
...                                   method=GraphTraversalMethod.HOP))
>>> ent_ancs = list(adapter.ancestors("GO:0012505",
...                                   method=GraphTraversalMethod.ENTAILMENT))
>>> len(hop_ancs), len(ent_ancs)
(9, 8)

This time the HOP strategy gives us one additional ancestor. We can see which one:

>>> set(hop_ancs) - set(ent_ancs)
{'PATO:0001735'}

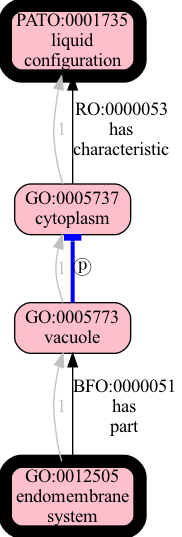
Figure generated using runoak   --stacktrace  -i tests/input/entailment-tutorial-2.obo paths "endomembrane system" @ PATO:0001735  --viz --directed --include-predicates

On the one hand this increased recall can be seen as an advantage of HOPping over a graph. On the other, the relationship between endomembrane system and liquid is not particularly meaningful, and may even be misleading (the endomembrane system is not itself liquid). If we decided that there is a meaningful named relation we want to use, then we can name it and define it with a property chain, and add it. E.g.

• has_part_with_characteristic <- has-part o has-characteristic

But this would be a fairly odd predicate with many entailed edges (e.g. a human body would stand in this relationship type to just about every property imaginable, e.g charges of all chemicals, morphologies of all cells, …).

On the other hand there are cases where the ontology developers have not anticipated all possible property chains, and in these cases the graph traversal strategy may yield potentially useful results.

Which strategy should I use?

The entailment strategy will give you more precise, meaningful results, but it may miss entailed edges you care about, especially if the ontology you are using does not make extensive use of property chains.

The graph traversal strategy will give you more complete results, the resulting paths may be meaningless, especially if you don’t constrain the predicates.

A note on entailed direct edges

Note

This is a fairly advanced topic that isn’t necessary for working with most ontologies.

Readers who are coming from an advanced OWL background may at this point be wondering why we don’t mention another category of entailed edges, specifically Direct edges that are entailed, but not Asserted.

For example, if we have an ontology with edges:

• MesentericVein drains SmallIntestine (or in OWL: MesentericVein SubClassOf drains some SmallIntestine)

• drains Domain Vein

Then OWL entailment will yield an edge:

• MesentericVein rdfs:subClassOf Vein

This may be a direct edge (if there is not a more specific vein classification), and in principle it may be the case that this is not asserted

However, OAK is designed for working with released versions of ontologies, which should be pre-classified. This means that all edges that are both Direct and Entailed should also be Asserted.

Further notes on OWL and Graph Projection

Many ontologies use the OWL language to express relationships between entities. The OWL representation is not directly a graph, but different kinds of OWL axioms can be projected onto graph edges. This kind of projection is common, but lacks standardization.

Two of the most common patterns in OWL ontologies are:

• SubClassOf between two named classes (e.g. Finger SubClassOf Digit)

• SubClassOf between a named class and a simple existential restriction (e.g. Digit SubClassOf part-of some Hand)

It’s a de-facto standard that these are both projected to graph edges (the former to an is-a or SubClassOf edge, the latter to a part-of edge). This can be seen e.g. in ontology browsers such as the OLS. These two kinds of axioms are very common in bio-ontologies. However, there is a lack of standardization in how more complex axioms should be mapped to edges, or whether they should be.

The following table outlines some common patterns and whether these are projected to edges in common tools:

OWL to Graph Projections

OWL Axiom	Graph Projection	SQL Adapter	Relation Graph
A SubClassOf B	rdfs:subClassOf B	Yes	Yes
A SubClassOf R some B	A R B	Yes	Yes
A SubClassOf R value B	A R B	Yes	No
A SubClassOf R only B	A R B	No	No
A SubClassOf R max 0 B	A R B	No	No
I type A	I rdf:type A	Yes	No
I type R some A	I R A	Yes	No
I type R value A	I R A	Yes	No
I Facts: R J	I R J	Yes	No

See OWLStar for progress towards a standardization of OWL graph projections for property graphs - this also includes proposals for labeling edges with axiom types as well as additional semantic information (e.g. cardinality) and annotations.